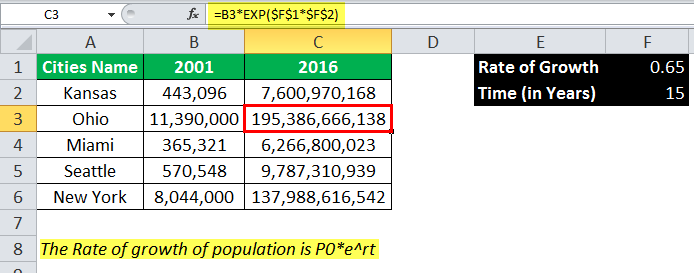
Y = e x For example 5 can be written as e 16 (the exponent is approximate) How do we know that this is the correct power of e?The following values represent exponential function ƒ(x) and linear function g(x) ƒ(1) = 2 g(1) = 25 ƒ(2) = 6 g(2) = 4 A Determine whether or not there is a solution to the equation In 23 sentences describe whether there is a solution to the equation ƒ(x)=g(x) between x=1 and x=2 B Use complete sentences to justify your claimOtherwise, the improper integral diverges Previous Numerical Integration
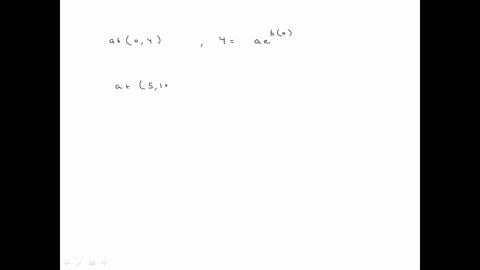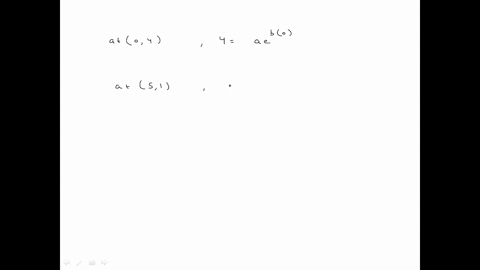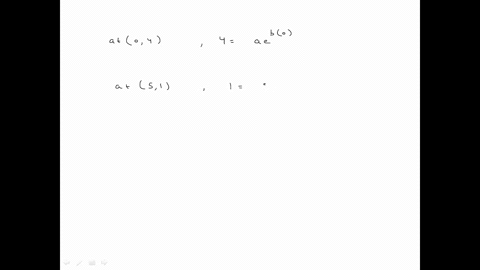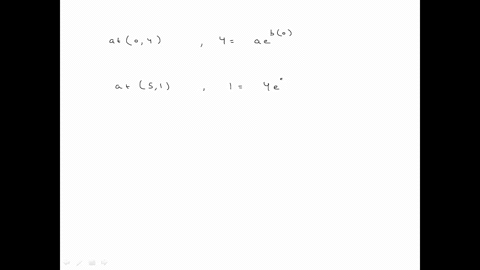
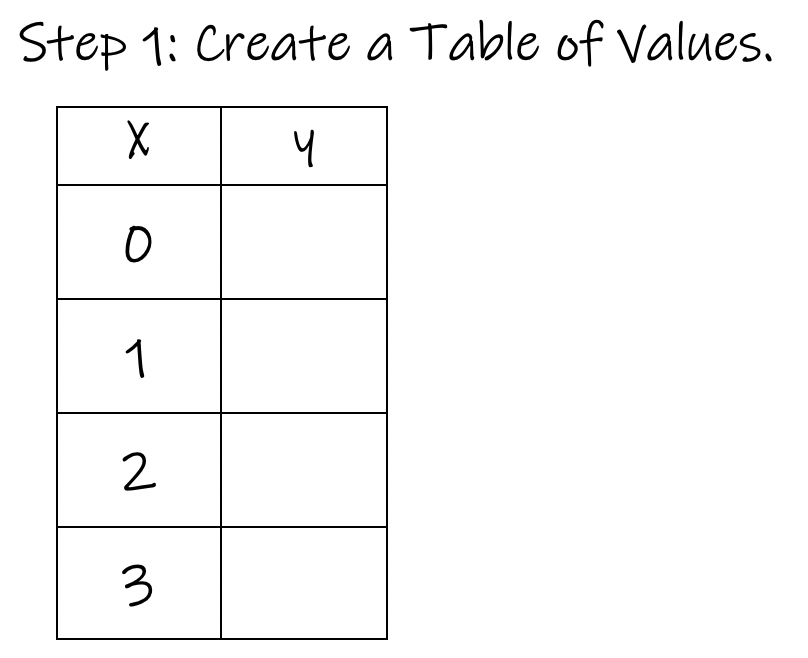
Solved A Make A Table Of Values For Y E X Usi
Y=e^x table of values
Y=e^x table of values-The exponential function can be easily described using this constant, for example, y = e x so as the value of x varies, then we can calculate the value of y Full value of e The value of Euler's number has a very large number of digits It can go 1000 digits placeIn Table 111, we list some rational numbers approaching 2, 2, and the values of 2 x 2 x for each rational number x x are presented as well We claim that if we choose rational numbers x x getting closer and closer to 2, 2, the values of 2 x 2 x get closer and closer to some number L L We define that number L L to be 2 2 2 2



How To Graph And Transform An Exponential Function Dummies
In mathematics, the exponential function is the function =, where e = 2718 is Euler's number More generally, an exponential function is a function of the form =,where b is a positive real number, and the argument x occurs as an exponent For real numbers c and d, a function of the form () = is also an exponential function, since it can be rewritten as$1 per month helps!!True Note that the t values are equally spaced and the ratios 3 0 0 1 4 7 = 1 4 7 7 2 0 3 = = 1 7 2 9 4 4 8 4 7 2 6 ≈ 2 0 4 are fixed so the function is exponential False Try again, although the ratios are fixed the t values are not evenly spaced False Try again, the t values are evenly spaces but the ratios are not fixed
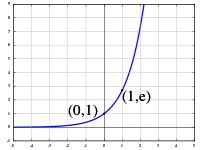
Write down a table showing the joint probability mass function for X and Y, find the marginal distribution for Y, and compute E(Y) Here is a table showing the joint probability mass function, with the marginal distributionThe mean, expected value, or expectation of a random variable X is written as E(X) or µ X If we observe N random values of X, then the mean of the N values will be approximately equal to E(X) for large N The expectation is defined differently for continuous and discrete random variablesThe graph of y=2 x is shown to the right Here are some properties of the exponential function when the base is greater than 1 The graph passes through the point (0,1) The domain is all real numbers The range is y>0 The graph is increasing The graph is asymptotic to the xaxis as x approaches negative infinity
Adjust the yaxis so that it includes the value entered for "Y 2 =" Press GRAPH to observe the graph of the exponential function along with the line for the specified value of latexf\left(x\right)/latex To find the value of x, we compute the point of intersection Press 2ND then CALC**Z< some value, will just be the probability found on table **Z> some value, will be (1probability) found on table Normal Distribution Example Sums of Normals Sums of Normals Example Cov(X,Y) = 0 b/c they're independent Central Limit Theorem as n increases,We will go to the Charts




Absolute Value Review 1 5 5 X If



What Is The Domain And Range Of Y E X Socratic
17x erf xxerf xxerf xxerf x 160 210 260 310 161 211 261 311We will display, modify, and format our X and Y plots We will set up our data table as displayed below Next, we will highlight our data and go to the Insert Tab In Excel 13 and later, we will go to the Insert Tab;Answer to Fill out the table of values for each exponential equation 1 y=3^2x x y 2 1 0 1 2 2 y=e^x x y 2 1 0 1 2 3y=



Graphing Y Mx B



Graph Exponential Functions Using Transformations College Algebra
With 1 split we have 2 1 or 2 times as much With 4 splits we have 2 4 = 16 times as much As a general formula Said another way, doubling is 100% growth We can rewrite our formula like this It's the same equation, but we separate 2 into what it really is the original value (1) plus 100%The following table lists the values of functions F and G and of their derivatives F Prime and G prime for the xvalues negative 2 & 4 and so you can see 4x equals negative 2x equals 4 they give us the values of F G F Prime and G Prime let function capital F be defined as the composition of F and G it's lowercase F of G of X and they want us to evaluate F prime of 4 so you might immediatelyIn fact, the expected value of a random variable is also called its mean, in which case we use the notationµ X(µ istheGreeklettermu) 2



Exponential In Excel Formula Examples How To Use Exp Function



1
Table 21 It should be noted that many other random variables could also be defined on this sample space, for example, the square of the number of heads or the number of heads minus the number of tails A random variable that takes on a finite or countably infinite number of valuesSelect two values, and plug them into the equation to find the corresponding values Tap for more steps Choose to substitute in for to find the ordered pair Tap for more steps Replace the variable with in the expression Create a table of the and values Graph the line using the slope and the yintercept, or the points SlopeImproper integral an integral over an infinite interval or an integral of a function containing an infinite discontinuity on the interval;




Here Is A Table Of Values For Y F X Brainly Com




Math 10 Functions Unit Lesson 6 Table Of Values Ppt Download
Eq1) where E X {\displaystyle \operatorname {E} X} is the expected value of X {\displaystyle X} , also known as the mean of X {\displaystyle X} The covariance is also sometimes denoted σ X Y {\displaystyle \sigma _{XY}} or σ (X , Y) {\displaystyle \sigma (X,Y)} , in analogy to variance By using the linearity property of expectations, this can be simplified to the expected valueSolution We can construct a table with x values getting closer and closer to 2 and find the corresponding values of ƒ1x2 LE 1 The table suggests that, as x gets closer and closer to 2 from either side, ƒ1x2 gets closer and closer to 4 In fact, you can use a calculator to show the values of ƒ1x2 can be made asThis might feel a bit more difficult to graph, because just about all of my yvalues will be decimal approximationsBut if I round off to a reasonable number of decimal places (one or two is generally fine for the purposes of graphing), then this graph will be fairly easy
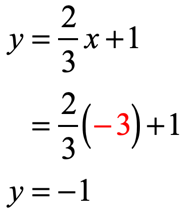



Graph A Line Using Table Of Values Chilimath



Exponentiation Wikipedia
The table shown gives selected values of a function f The function is twice differentiable with f ''(x) > 0 Which of the following could be the value of f '(3)?Y = (E(X) X) (E(Y) Y) = ( X X) ( Y Y) = 0 This does NOT mean If covariance=0, then Xand Y are independent We can nd cases to the contrary of the above statement, like when there is a strong quadratic relationship between Xand Y (so they're not independent), but you can still get ˙XY = 0 Remember that covariance speci cally looks forStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Problem 4 The Random Variable X Has A Range Of 10 Chegg Com
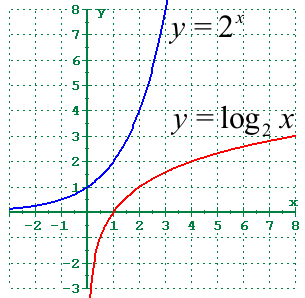



4 2 Logarithmic Functions And Their Graphs
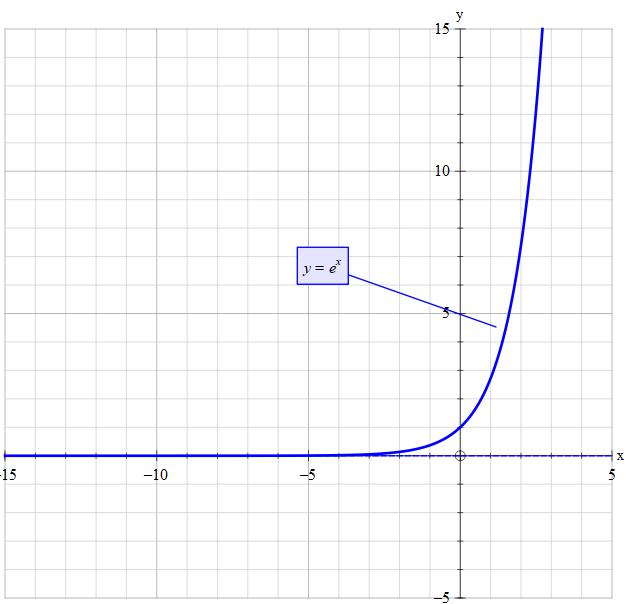
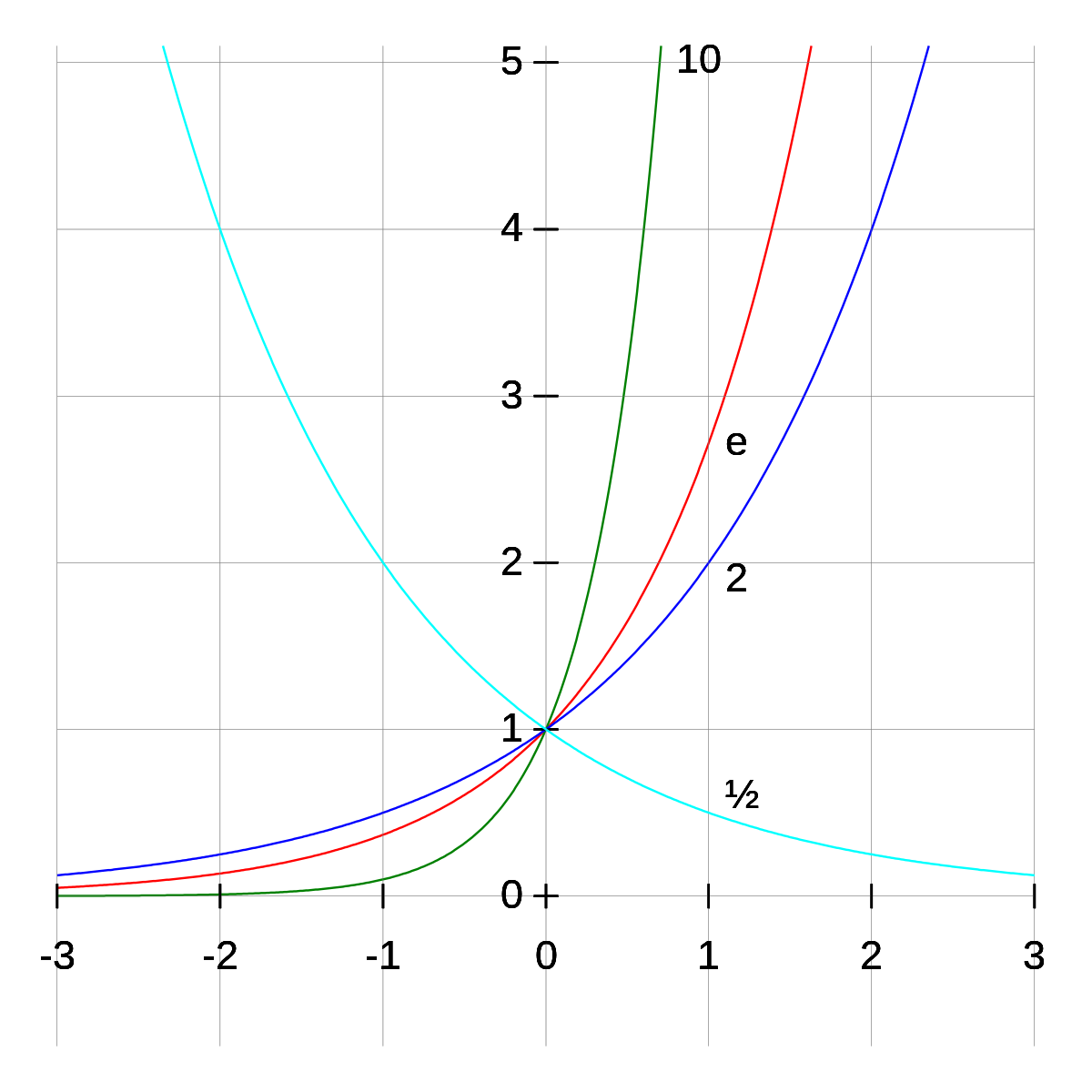
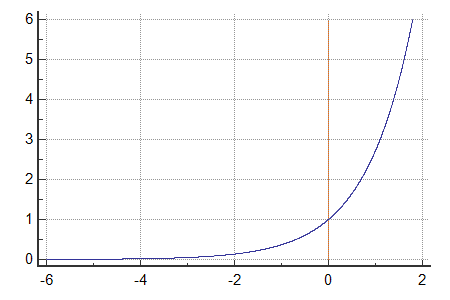
A graph of the exponential function y = ex It is important to note that as x becomes larger, the value of ex grows without bound We write this mathematically as ex → ∞ as x → ∞ This behaviour is known as exponentialgrowth Thenegativeexponentialfunction A related function is the negativeexponentialfunctiony = e−x A table of valuesAnswer choices 0405 0768 1500Excel Plot X vs Y We will set up a data table in Column A and B and then using the Scatter chart;



Logarithmic And Exponential Graphs
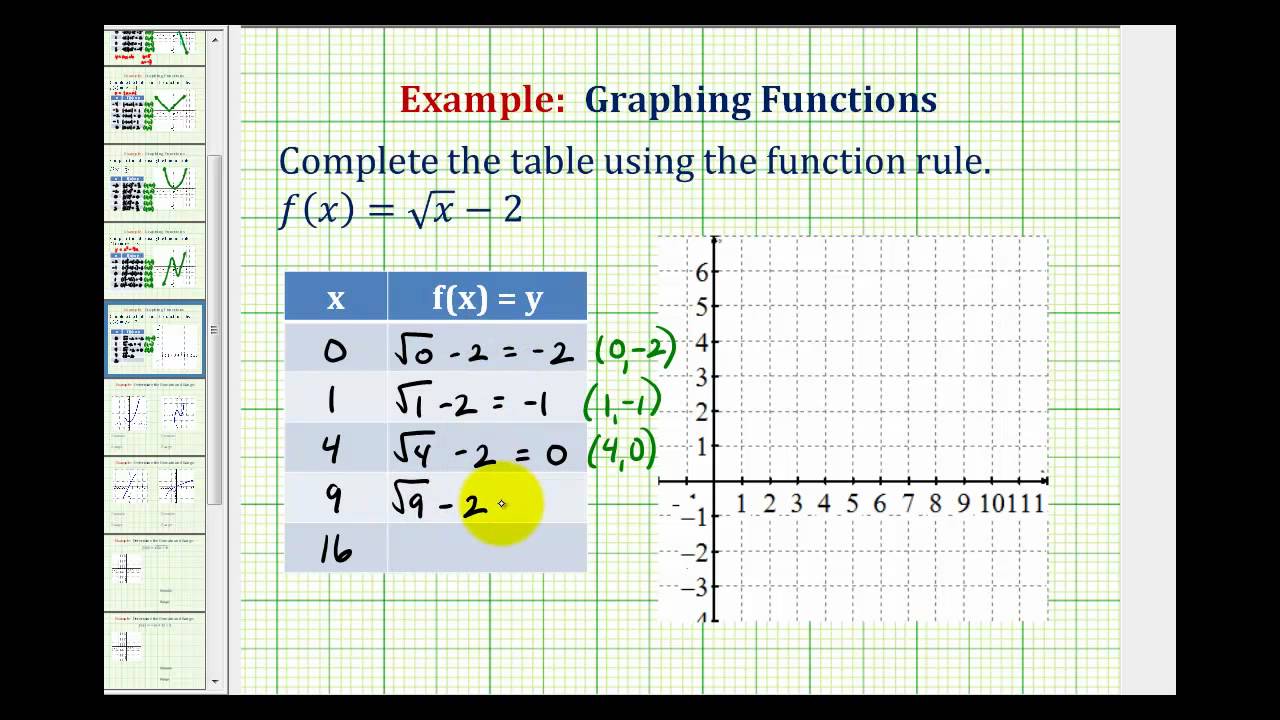



Ex Graph A Square Root Function Using A Table Of Values Youtube
Rather it is a weighted average of the possible values 3 Expected value is a summary statistic, providing a measure of the location or central tendency of a random variable 4 If all the values are equally probable then the expected value is just the usual average of the values Example 3 Find E(X) for the random variable X with table 0 You can use the definition of an expectation E (XY) = x*y*f (x,y) dy dx Or you could argue that since the function is symmetric about 0 and the intervals 1, 1 are centred about 0 that E (XY) = 0The table below shows the value of a predicate M(x, y) for every possible combination of values of the variables x and y The domain for x and y is {1, 2, 3} The row number indicates the value for x and the column number indicates the value for y For example M(1, 2) = F because the value in row 1, column 2, is F
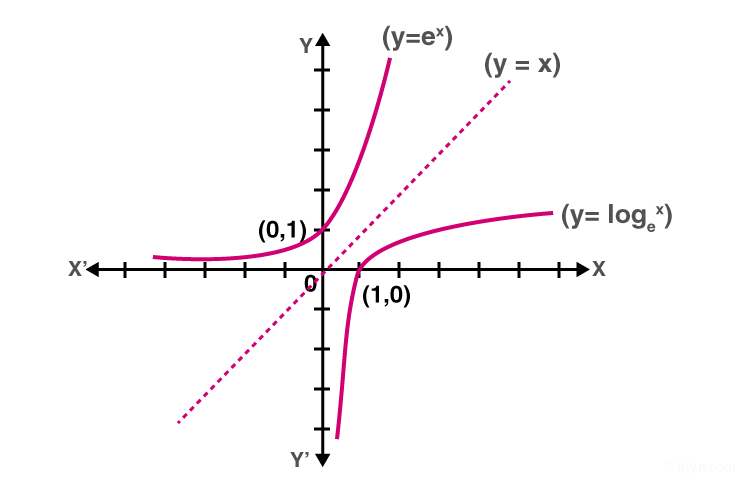



Exponential Functions Definition Formula Properties Rules
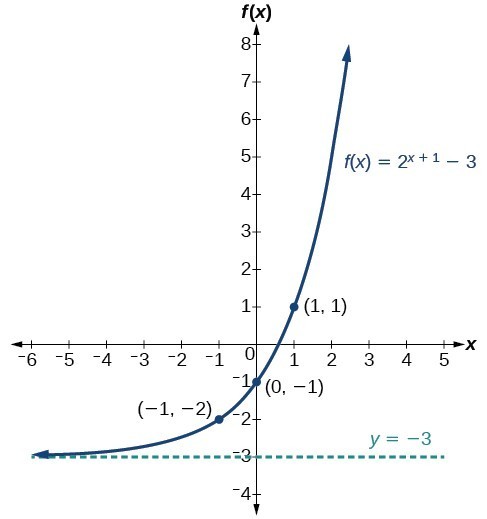



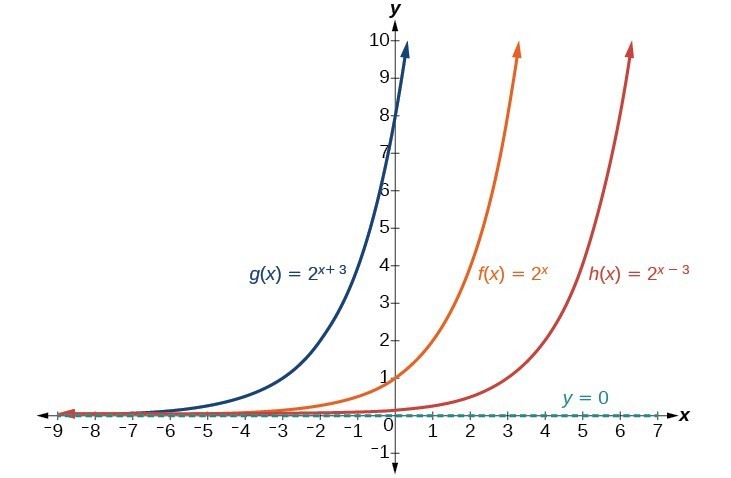
Graph Exponential Functions Using Transformations College Algebra
Line l is tangent to the graph of y = e x at the point (k, e k) What is the positive value of k for which the yintercept of l is 1/2?I am studying probability and trying to follow an example in my textbook discussing expectation of the sum of random variables But I'm having trouble following it E X Y = ∫ − ∞ ∞ ∫ − ∞ ∞ (xy)f (x,y)dxdy = ∫ − ∞ ∞ ∫ − ∞ ∞ x f ( x, y) d y d x ∫ − ∞ ∞ ∫ − ∞ ∞ y f ( x, y) d x d y = ∫ −So as we know about the exponents, this Exponential Function in Numpy is used to find the exponents of 'e' We know that the value of 'e' is ''
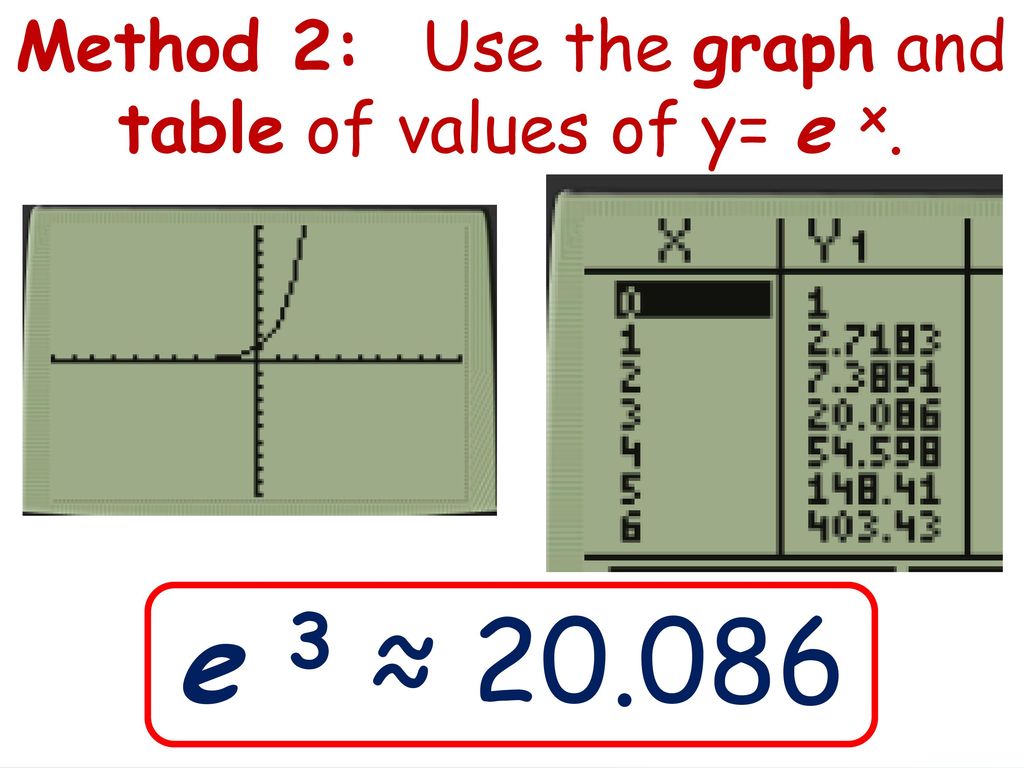



A Sse A 1b Interpret Expressions That Represent A Quantity In Terms Of Its Context Interpret Complicated Expressions By Viewing One Or More Of Their Ppt Download



Q Tbn And9gctedl8udcqjh7vkimoh2eiobltvx3 Lmqnuxqxbgyaeanqealrk Usqp Cau
Variable which is a function of Y taking value E(XjY =y) when Y =y The E ( g ( X ) jY ) is defined similarly In particular E ( X 2 jY ) is obtained when g ( X )= X 2 andGraph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0How to find natural logarithms with a table or a calculator An explanation of how to use a table to find "Function Values for e^x and e^x" Making a table
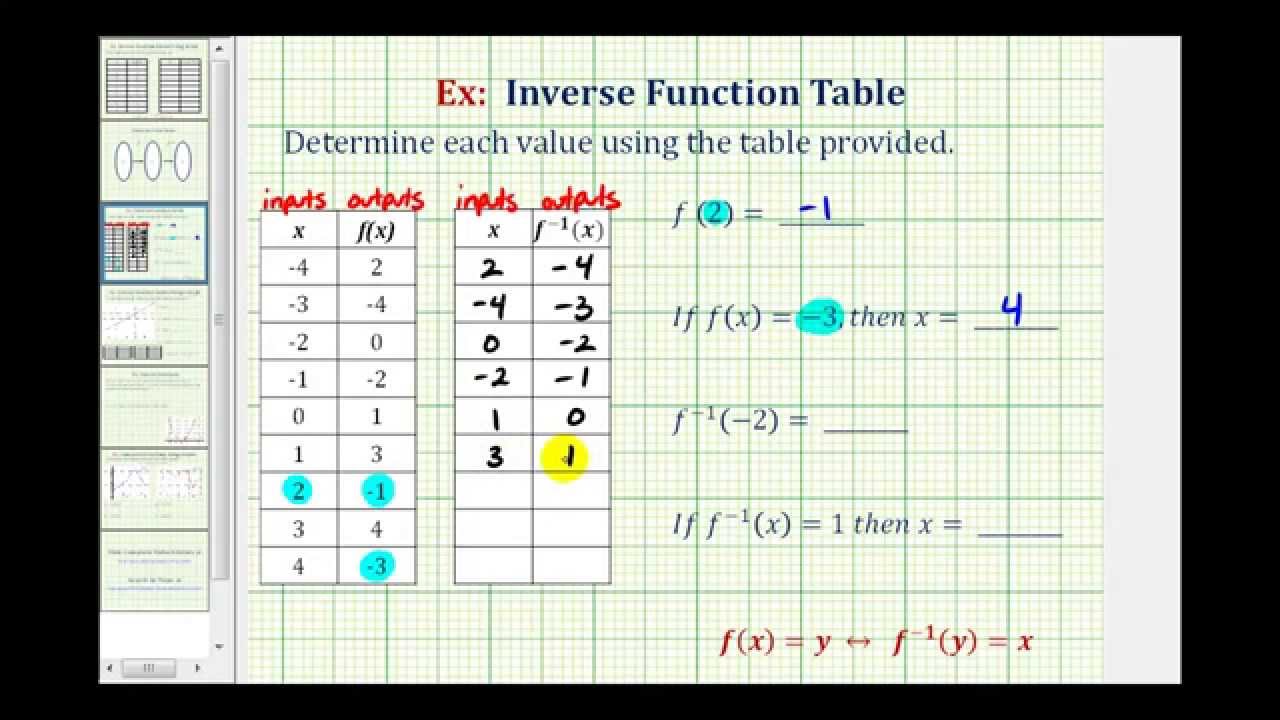



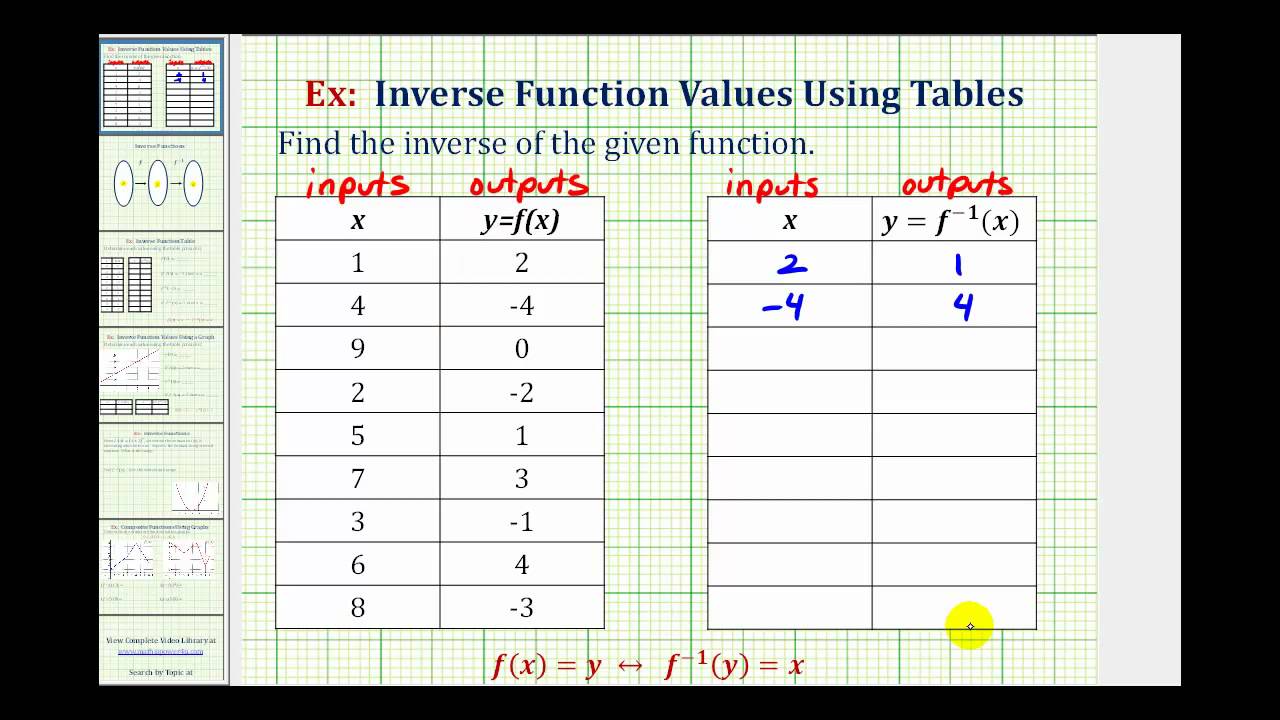
Ex Function And Inverse Function Values Using A Table Youtube




Complete The Table Of Values For Y 2 X Brainly Com
The expected value of the random variable EXjY It is a function of Y and it takes on the value EXjY = y when Y = y So by the law of the unconscious whatever, EEXjY = X y EXjY = yP(Y = y) By the partition theorem this is equal to EX So in the discrete case, (iv) is really the partition theorem in disguise In the continuous caseGraph of y = e ^ (x 3) u1 The expected value of a random variable is denoted by EX The expected value can bethought of as the"average" value attained by therandomvariable;




Orgattachment9562 Docviewer 90 12 Sin2x 11 Y E 13 J Sec2x 14 Selected Values Of The Differentiable Functions F And G And Selected Values Of Their First Derivatives Are Given In The Table



1
Enter values into the coordinate tool and the values will automatically update For decimal degrees, remember to include the negative sign for south and west coordinates!The possible values of Xare 129, 130, and 131 mm The possible values of Yare 15 and We show the probability for each pair in the following table x=length 129 130 131 y=width 15 012 042 006 16 008 028 004 The sum of all the probabilities is 10 The combination with the highest probability is (130;15) The combination with theAs with part iv of the logarithm properties, we can extend property iii to irrational values of r, r, and we do so by the end of the section We also want to verify the differentiation formula for the function y = e x y = e x To do this, we need to use implicit differentiation Let y = e x y = e x Then



Canvas Dartmouth Edu Courses Files Download Verifier Osd8tfnd6hdd05ls4hr0iwrbxmarelhxvgi7tovn Wrap 1



Example 1 The Natural Base
Graph y = e x;9Using the lefthand Riemann sum with n= 4, approximate Z 9 1 1 x dx Answer Z 9 1 1 x dxˇ2 1 1 1 3 1 5 1 7 = 352 105 10Suppose that f(2) = 4, and that the table below gives values of f0for xin the interval 0;12The difference is that in the first case it is about "values of" and in the second you consider a certain value You could find the diagram below helpful Share




Complete The Tables Of Values For Y 6 X Brainly Com
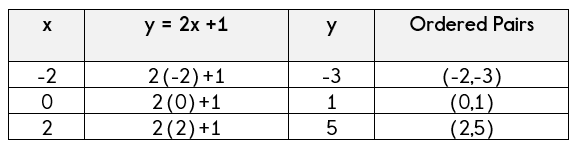



Using A Table Of Values To Graph Equations
Summary f (x) = e x is the natural base exponential function 'e' is the natural base ' ≈ ' means 'approximately equal to' Plug each 'x' value into e x You can either use the 'e' button on your calculator or use the approximation 2718 for 'e' to find each value f (x) = e x has a horizontal asymptote along the xaxisDefinition 2 The exp function E(x) = ex is the inverse of the log function L(x) = lnx L E(x) = lnex = x, ∀x Properties • lnx is the inverse of ex ∀x > 0, E L = elnx = x • ∀x > 0, y = lnx ⇔ ey = x • graph(ex) is the reflection of graph(lnx) by line y = x • range(E) = domain(L) = (0,∞), domain(E) = range(L) = (−∞,∞)Easy Tutor author of Program to print table of values of the function y = e raise to x is from United StatesEasy Tutor says Hello Friends, I am Free Lance Tutor, who helped student in completing their homework I have 4 Years of hands on experience on helping student in completing their homework I also guide them in doing their final year projects



6 Derivative Of The Exponential Function
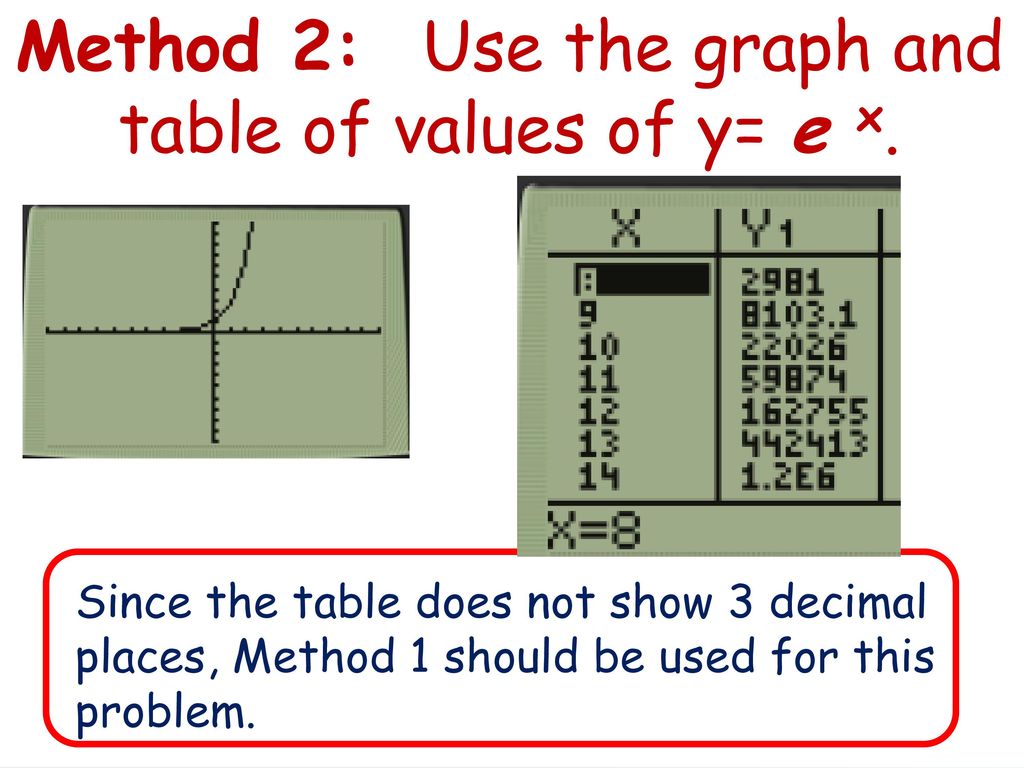



A Sse A 1b Interpret Expressions That Represent A Quantity In Terms Of Its Context Interpret Complicated Expressions By Viewing One Or More Of Their Ppt Download
Hi, guys today we have got a very easy topic ie exponential function in Numpy – Python So let's start The first question comes in our mind that what is the Exponential Function and what it does?WolframAlpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook It uses wellknown rules such as the linearity of the derivative, product rule, power rule, chain rule and so on Additionally, D uses lesserknown rules to calculate the derivative of a wideErrors will show in red text Latitude (90 to 90) and longitude (180 to 180) Include up to 6 decimal places




Exponential Function Wikipedia




What Is The Expected Value Of The Expected Of X Conditional Of Y E E X Y And Also If Possible E X 2 Y Cross Validated
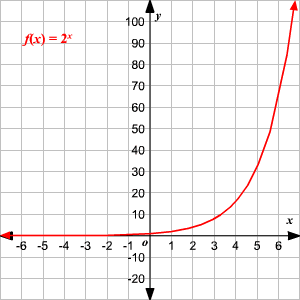
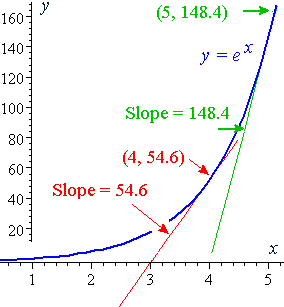
Just think about the x, y values in the table above At, say, an output value, or y value, of 1,000,000 the input would not be 0 And, of course, the input value, or x value, must be 0 for the graph to touch the yaxis This type of behavior about the yaxis is called asymptotic behaviorBecause we get it from the graph shown below To make this graph we made a table of a few obvious values of y = e x as shown below, left Then we plotted the values in the graph (they are the red dots) and drew aWe've been given some inch for interesting information here about the functions F G and H for F they tell us for given values of X what f of X is equal to and what F prime of X is equal to then they define G of X for us in terms of this kind of absolute value expression and then it define H of X for us in terms of both f of X and G of X and what we're curious about is what is the derivative



6 Derivative Of The Exponential Function
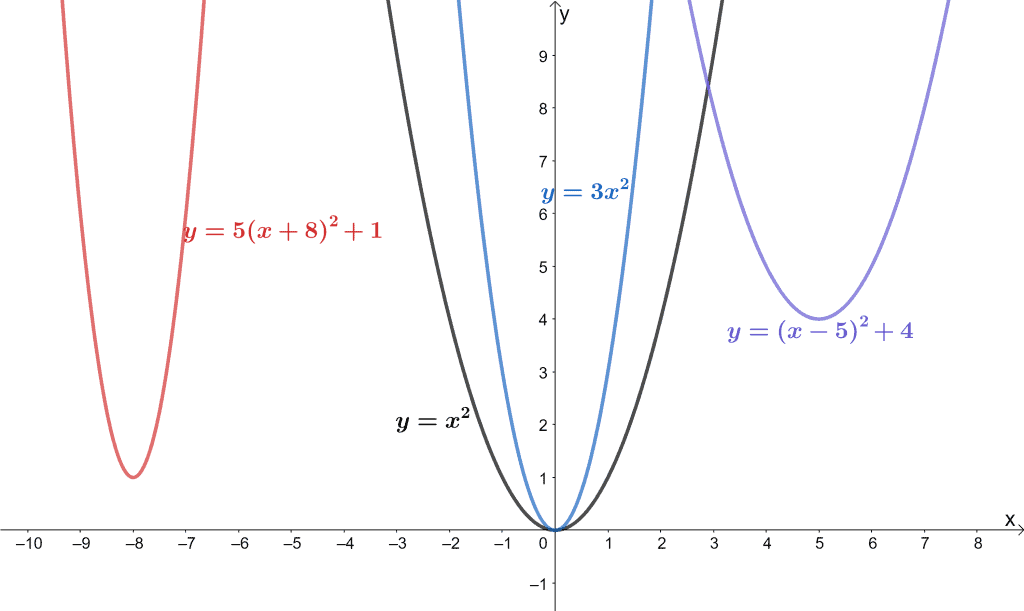



Parent Functions Types Properties Examples
To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form f(x) = bx f ( x) = b x whose base is between zero and one We'll use the function g(x) = (1 2)x g ( x) = ( 1 2) x Observe how the output values in the table below change as the input increases by 1 xAn improper integral is defined in terms of a limit The improper integral converges if this limit is a finite real number;Thanks to all of you who support me on Patreon You da real mvps!



Matlab Plotting Tutorialspoint



Ex Find An Inverse Function From A Table Youtube



Wll Tueaa994qm



Domain And Range Of Exponential And Logarithmic Functions



Http Www Sfu Ca Rpyke Math251 Hw 14 4a Pdf




Absolute Value Review 5 X If X 2 6 X 3 If X Ppt Video Online Download



Exp Exponential Function Calculator And Graph



Exponential Function Wikipedia




Complete The Table Of Values For The Function F X 1 X Brainly Com



6 Derivative Of The Exponential Function




Intro To Exponential Functions Algebra Video Khan Academy



6 Derivative Of The Exponential Function



Absolute Value Review 1 5 5 X If



Solved A Make A Table Of Values For Y E X Usi
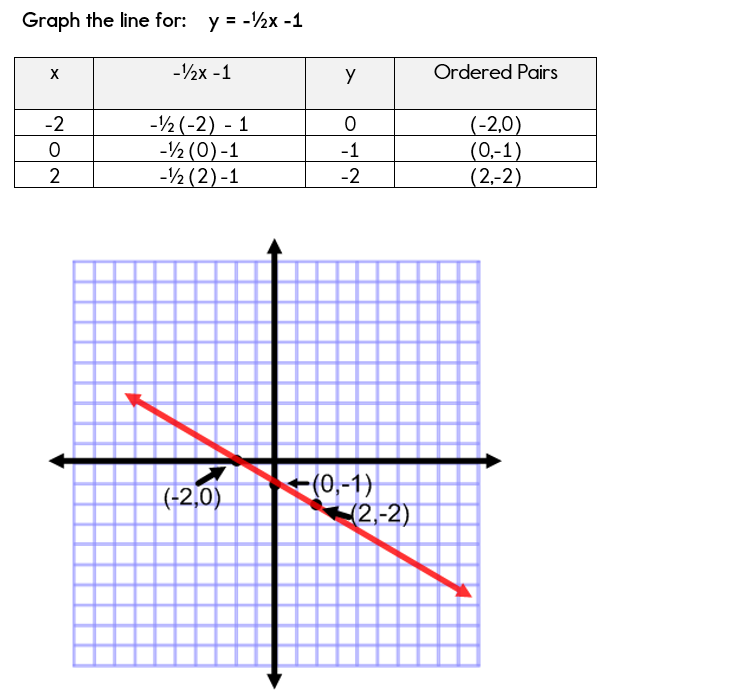



Using A Table Of Values To Graph Equations
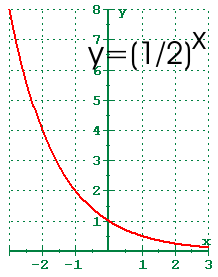



4 1 Exponential Functions And Their Graphs



How Do You Solve An Exponential Equation With E As The Base Youtube



Ex Find A Trig Function From A Table Of Values No Phase Shift Youtube




2 1 11 8 Chapter 5




Mido8daduab58m



1



What Is The Table Of Values For Y X 2 Socratic
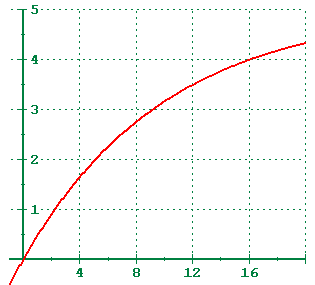



4 5 Exponential And Logarithmic Models



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch17 Pdf
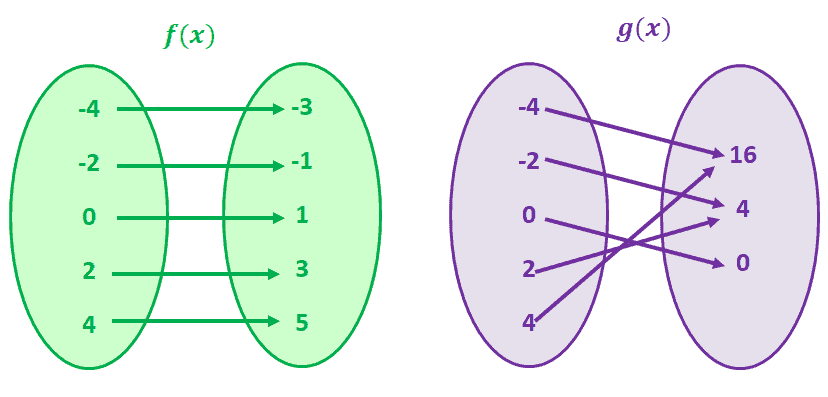



One To One Function Explanation Examples
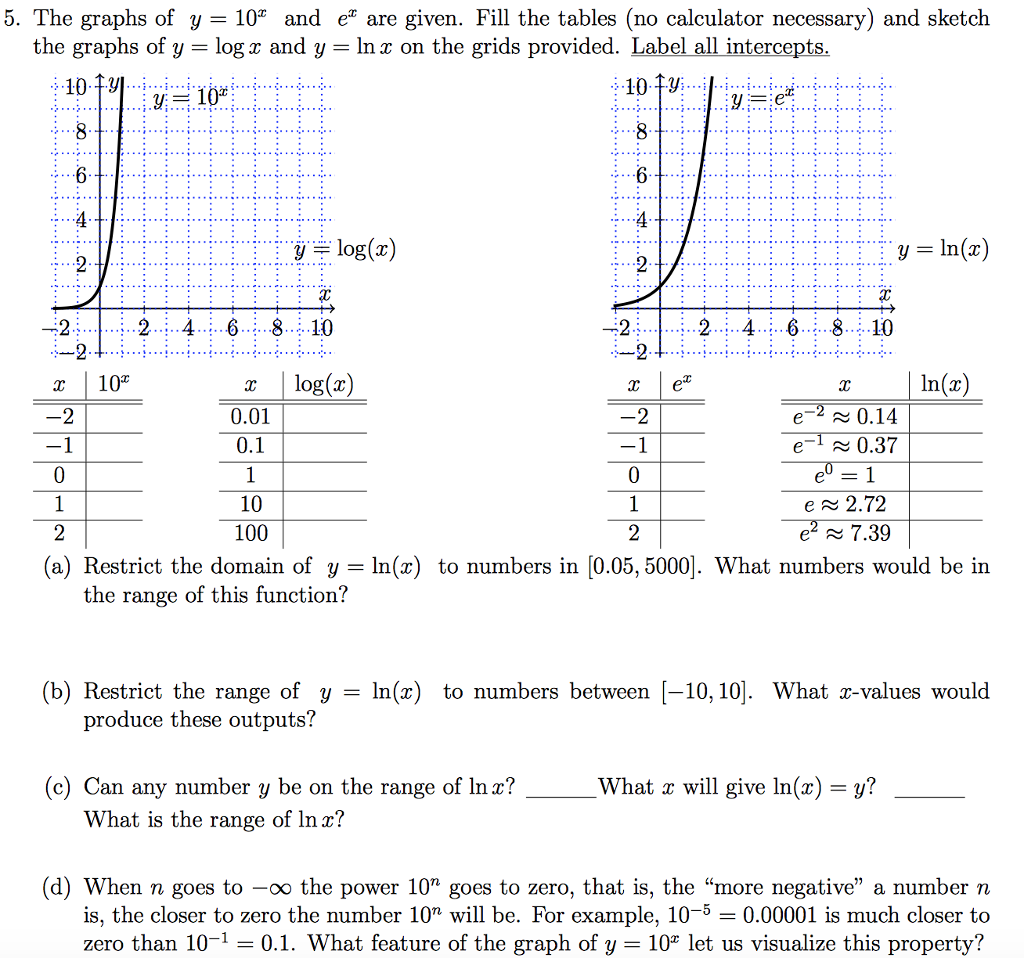



5 The Graphs Of Y 10 And Ex Are Given Fill The Chegg Com




Graph A Linear Equation Using A Table Of Values Studypug
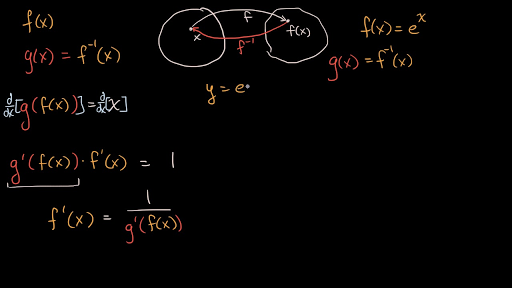



Derivatives Of Inverse Functions Video Khan Academy




2 1 11 8 Chapter 5
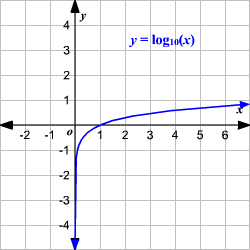



Logarithmic Functions
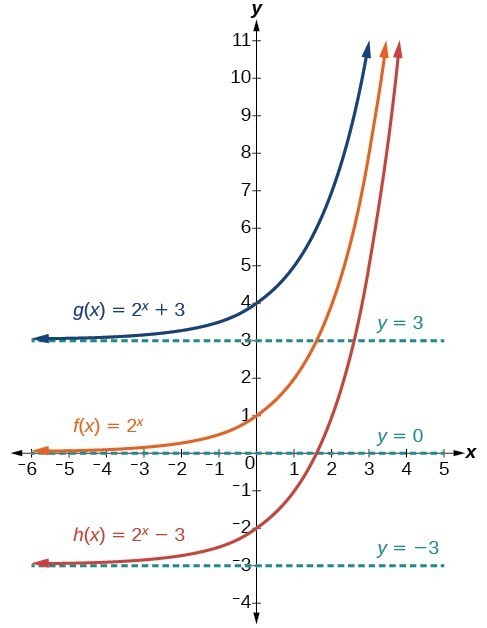



Graph Exponential Functions Using Transformations College Algebra
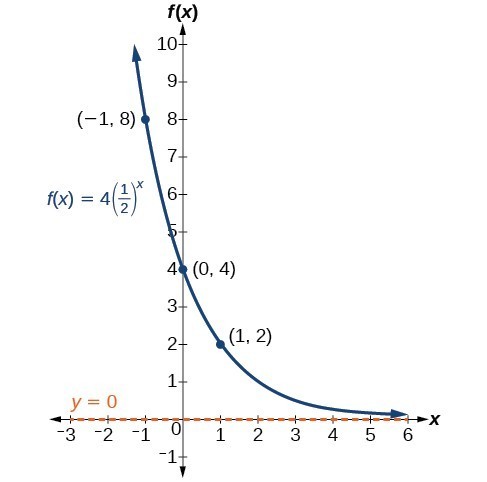



Graph Exponential Functions Using Transformations College Algebra
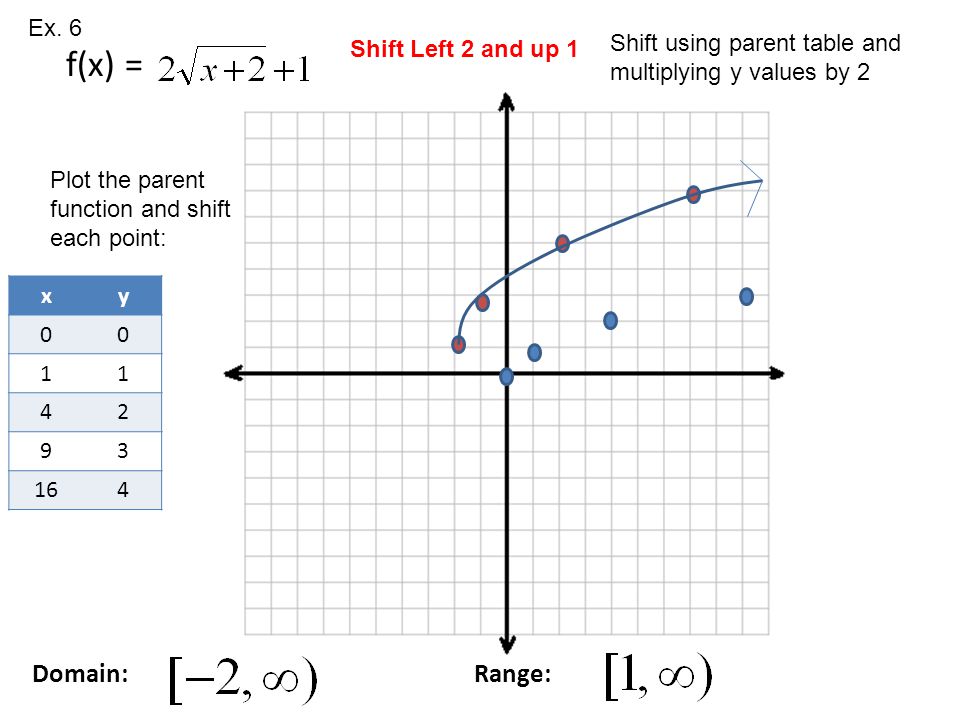



Day 5 Book Section 7 8 Get 2 Grids For The 2 Shift Problems Ppt Download



Graph A Line Using Table Of Values Chilimath



Exponential Functions The Natural Exponential E




Completing A Table Of Values Youtube




rushi Karandikar Akhil Aji Eugene Kim Taleen Boghossian Period 4 Ppt Download




Ex Determine If A Table Of Values Represents A Function Youtube
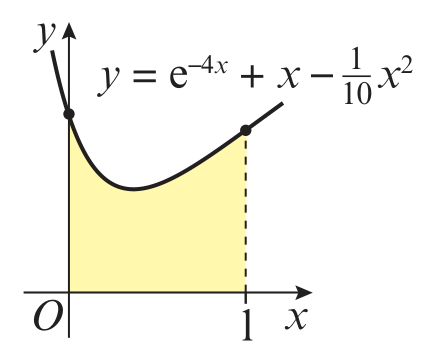



The Diagram Shows A Sketch Of Part Of The Curve With Equation Y E 4x X Dfrac 1 10 X 2 Use The Trapezium Rule With All The Y Values In The Completed Table To Obtain An Estimate For The




For Section 3 1 1 Create A Table Of Values And Chegg Com




Solved A Make A Table Of Values For Y E X Usi
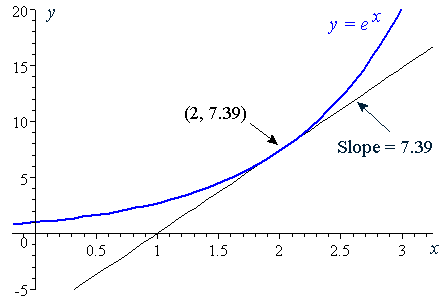



6 Derivative Of The Exponential Function




Reference Values Of Moduli Of Elasticity E X E Y And In Plane Shear Download Table




The Optfmai Stock X Harvest Y And Effort E In The Download Table




Worked Example Average Rate Of Change From Table Video Khan Academy




Solved A Make A Table Of Values For Y E X Usi
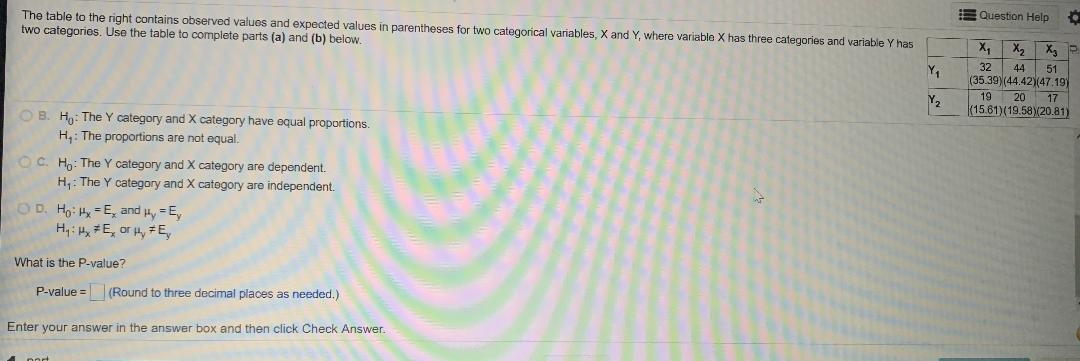



Answered The Table To The Right Contains Bartleby
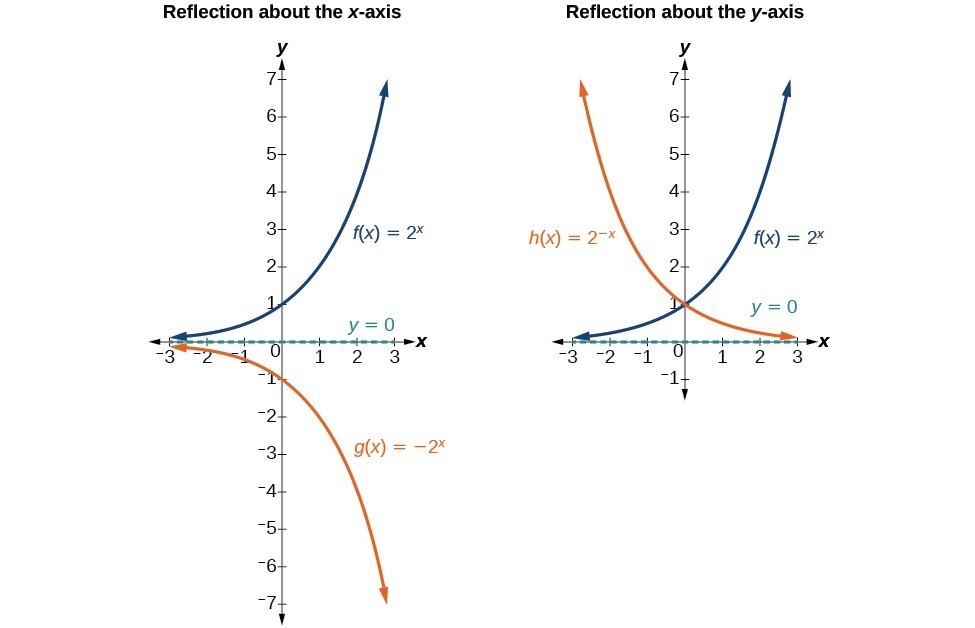



Graph Exponential Functions Using Transformations College Algebra



Http Www Stat Wisc Edu Ifischer Calculus Pdf




Ex 1 Graph A Linear Equation Using A Table Of Values Youtube
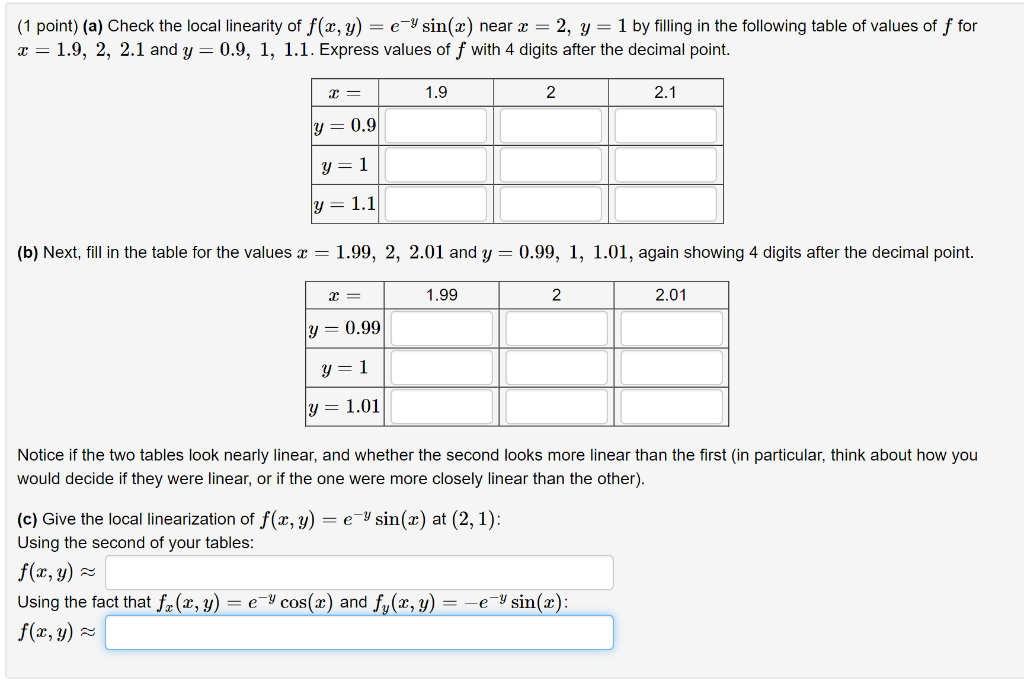



Solved 1 Point A Check The Local Linearity Of F X Y Chegg Com




Question Video Completing Tables Of Values For Functions Nagwa
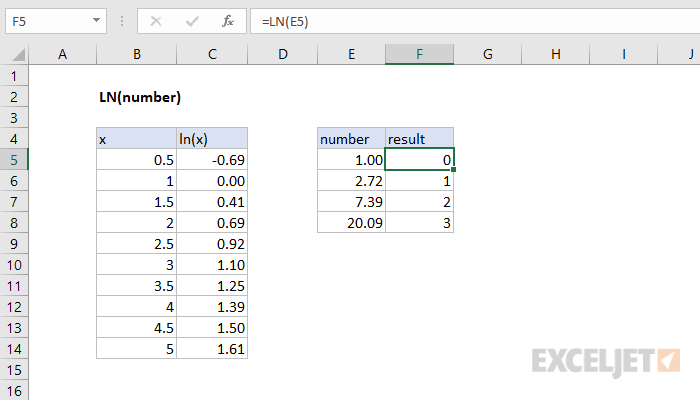



How To Use The Excel Ln Function Exceljet
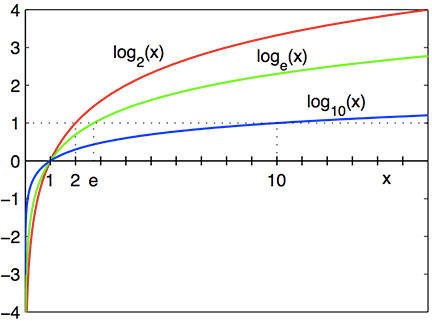



Graphs Of Exponential And Logarithmic Functions Boundless Algebra
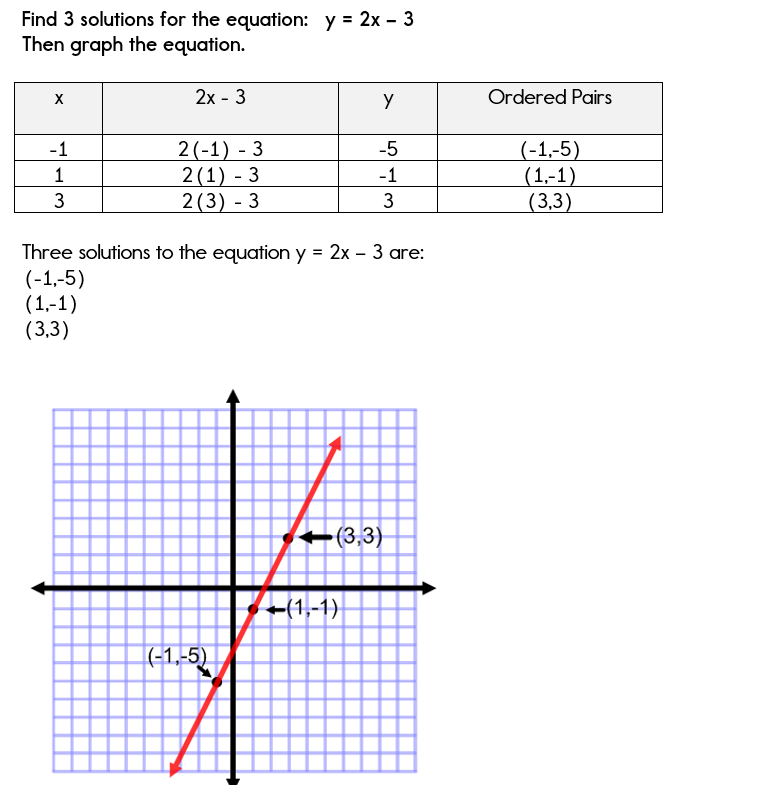



Using A Table Of Values To Graph Equations




How To Graph And Transform An Exponential Function Dummies
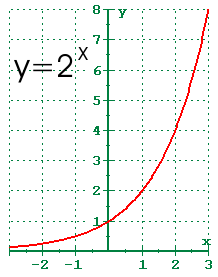



4 1 Exponential Functions And Their Graphs




Solved 1 Point A Check The Local Linearity Of F X Y Chegg Com




Chapter Five A Joint Probability Distributions And Random Samples




Check The Local Linearity Of F X Y Ex Cos Y Near Chegg Com
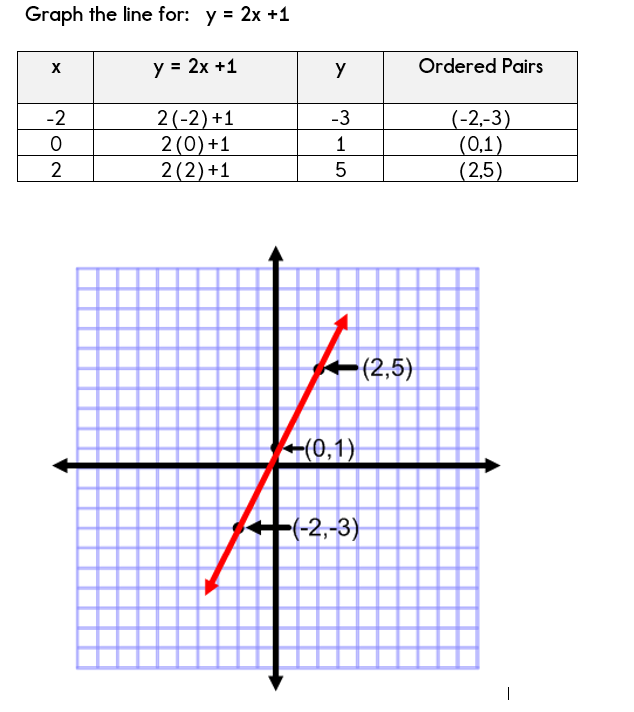



Using A Table Of Values To Graph Equations
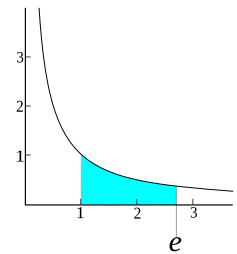



E Mathematical Constant Wikipedia




Ex Graph A Quadratic Function Using A Table Of Values Quadratics Graphing Functions Quadratic Functions




69 Consider The Table Of Values For The Chegg Com



Whs Wwusd Org Page 4341 216 Notes 401 2413
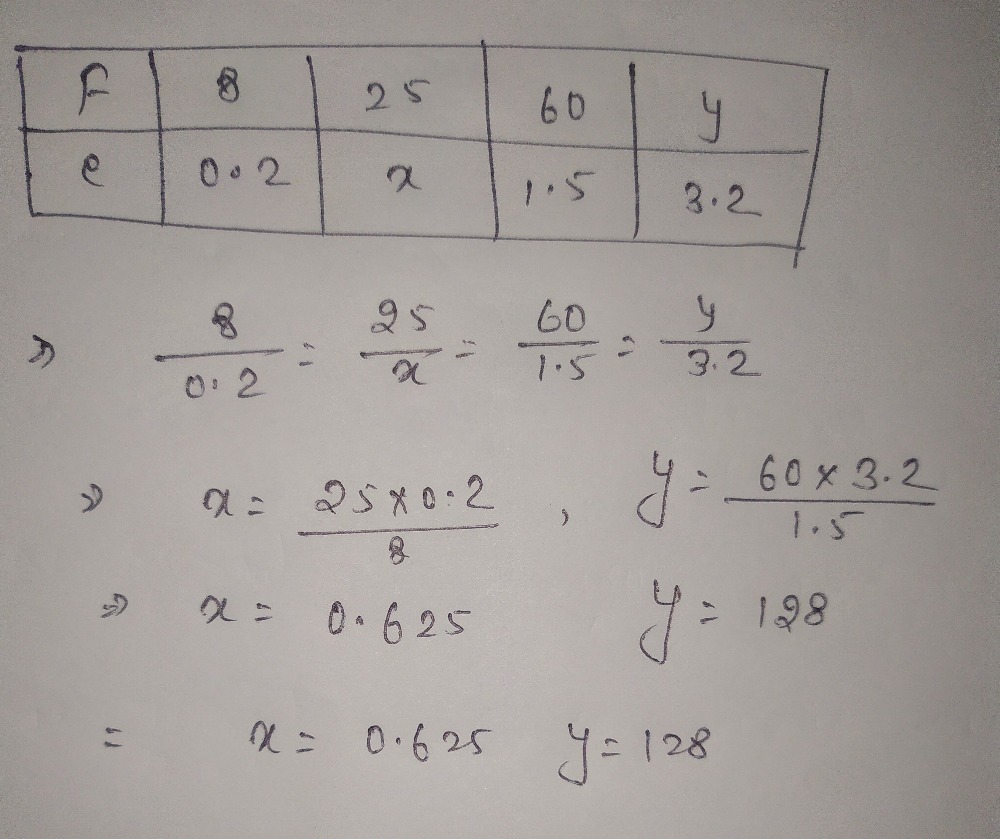



The Incomplete Table Below Shows Corresponding Val Gauthmath
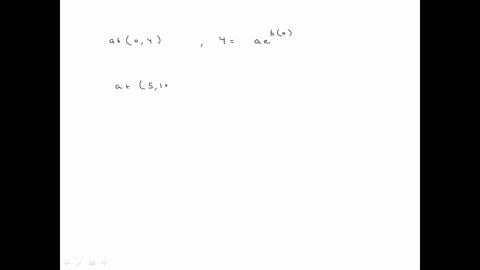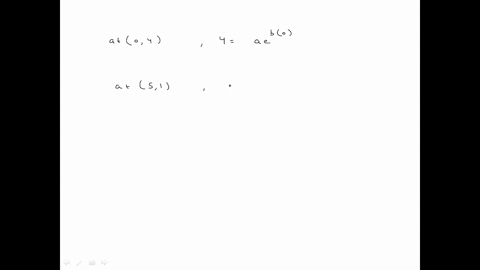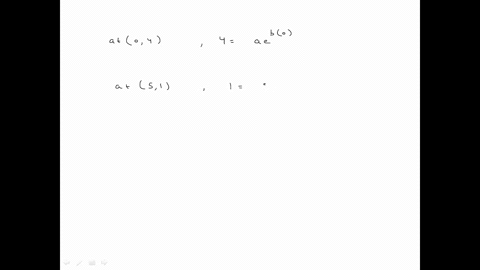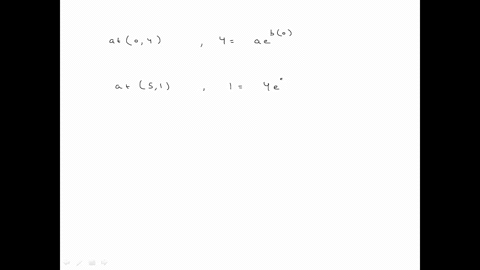



Solved A Make A Table Of Values For Y E X Usi
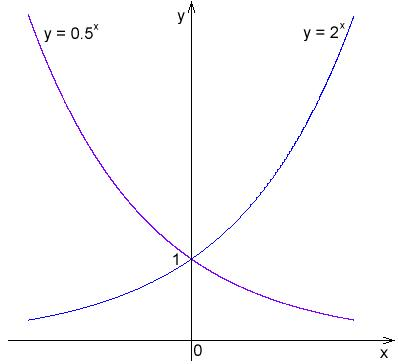



Graphs Of Exponential And Logarithmic Functions Boundless Algebra




8 3 Logarithm Functions As Inverses Hubarth Algebra Ii Ppt Download




How To Graph And Transform An Exponential Function Dummies




Using Transformations To Graph Functions
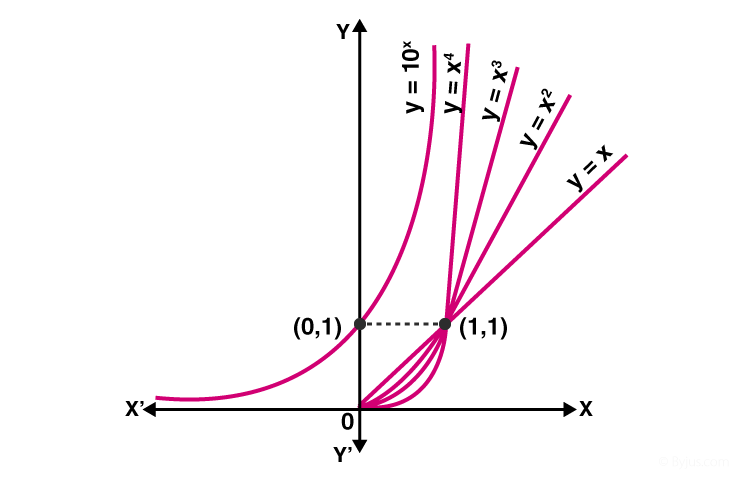



Exponential Functions Definition Formula Properties Rules



0 件のコメント:
コメントを投稿